Timeline Monoid

Super simple yet versatile Functional Reactive Programming(FRP) framework with a minimal implementation for monoidal Timeline datatype

npm package:

https://www.npmjs.com/package/timeline-monoid

Installation

$ npm install timeline-monoid

Usage

 const {T, now, log, mlong} = require("timeline-monoid");

Equations

   b = a * 2
   c = a + b

   a = 1 or a = 5
   a,b,c ?

code

    const a = T();
    const b = (a).sync(a => a * 2);
    const c = (a)(b).sync(([a, b]) => a + b);
    const abc = (a)(b)(c);

    const timeline = abc.sync(log);

    a[now] = 1;
    a[now] = 5;

output

[ 1, 2, 3 ]
[ 5, 10, 15 ]

Asynchronous programming

Any time functions which is generally called "events" or "asynchronous events" are encapsulated to timeline instance, and they are composed to another timeline instance.

Basic usage

      const fs = require("fs");
      const timelineA = T((timeline) => { // Event encapsulation
        fs.readFile("package.json", "utf8", (err, data) => {
          timeline[now] = data;
        });
      });
      const timelineB = T((timeline) => { // Event encapsulation
        fs.readFile("index.js", "utf8", (err, data) => {
          timeline[now] = data;
        });
      });
      const timelineAB = (timelineA)(timelineB) // Event Composition
        .sync(([a, b]) => {
          console.log("Async read: Files A and B are now ready");
        //console.log(a); //show file contents if needed
        //console.log(b); //show file contents if needed
        });

Lazy start and reusable event Timeline

    const startA = T();
    const startB = T();

    const timelineA = T((timeline) => {

      (startA)
        .sync(() => fs
          .readFile("package.json", "utf8", (err, data) => {
            timeline[now] = data;
          }));

    });

    const timelineB = T((timeline) => {

      (startB)
        .sync(() => fs
          .readFile("index.js", "utf8", (err, data) => {
            timeline[now] = data;
          }));

    });

Async read files on the reusable event Timeline

          const asyncStart = T();
          const context = asyncStart
            .sync(() => {
              startA[now] = true;
              startB[now] = true;
            });
          const contextAB = (context)(timelineA)(timelineB)
            .sync(([x, a, b]) => {
              console.log("Async read: Files A and B are now ready");
            //console.log(a); //show file contents if needed
            //console.log(b); //show file contents if needed
            });

          asyncStart[now] = true;

Sync read files on the reusable event Timeline

            const syncStart = T();
            const context = syncStart
              .sync(() => {
                startA[now] = true;
              });
            const contextA = (context)(timelineA)
              .sync(([x, a]) => {
                console.log("now A has been read");
                // console.log(a); //show file contents if needed
                startB[now] = true;
                return true;
              });
            const contextB = (context)(timelineB)
              .sync(([x, b]) => {
                console.log("then B has been read");
                // console.log(b); //show file contents if needed
                return true;
              });

            syncStart[now] = true;

Simple Mouse Draw on Canvas

Live Demo https://jsfiddle.net/5u9pLgme/8/

<canvas id="canvas1" width="900" height="500"></canvas>

    const canvas = document.getElementById('canvas1');
    const ctx = canvas.getContext('2d');
    const draw = ([x0, y0], [x1, y1]) => {
      ctx.beginPath();
      ctx.moveTo(x0, y0);
      ctx.lineTo(x1, y1);
      ctx.closePath();
      ctx.stroke();
    };

    const btnTimeline = T((timeline) => {
      canvas.onmousedown = (e) => timeline[now] = 1;
      canvas.onmouseup = (e) => timeline[now] = 0;
    });

    const pointTimeline = T((timeline) => {
      canvas.onmousemove = (e) => timeline[now] = [e.clientX, e.clientY];
    })

    const pipeline = pointTimeline
      .sync((point) => (btnTimeline[now] === 1)
        ? draw(lastPointTimeline[now], point)
        : true);

    const lastPointTimeline = T((timeline) => {
      pointTimeline.sync(point => {
        timeline[now] = point;
      });
    });

Background and Rationale

Functional Reactive Programming (FRP) integrates time flow and compositional events into functional programming.

The basic idea is that a time-varying value can be represented as a function of time.

Structure and Interpretation of Computer Programs(SICP) (Chapter 3.5 : Streams)

Let's step back and review where this complexity comes from. In an attempt to model real-world phenomena, we made some apparently reasonable decisions: We modeled real-world objects with local state by computational objects with local variables. We identified time variation in the real world with time variation in the computer. We implemented the time variation of the states of the model objects in the computer with assignments to the local variables of the model objects.

Is there another approach? Can we avoid identifying time in the computer with time in the modeled world? Must we make the model change with time in order to model phenomena in a changing world? Think about the issue in terms of mathematical functions. We can describe the time-varying behavior of a quantity x as a function of time x(t). If we concentrate on x instant by instant, we think of it as a changing quantity. Yet if we concentrate on the entire time history of values, we do not emphasize change -- the function itself does not change. (Physicists sometimes adopt this view by introducing the world lines of particles as a device for reasoning about motion.)

If time is measured in discrete steps, then we can model a time function as a (possibly infinite) sequence. In this section, we will see how to model change in terms of sequences that represent the time histories of the systems being modeled. To accomplish this, we introduce new data structures called streams. From an abstract point of view, a stream is simply a sequence. However, we will find that the straightforward implementation of streams as lists (as in section 2.2.1) doesn't fully reveal the power of stream processing. As an alternative, we introduce the technique of delayed evaluation, which enables us to represent very large (even infinite) sequences as streams.

This is really remarkable. Even though stream-withdraw implements a well-defined mathematical function whose behavior does not change, the user's perception here is one of interacting with a system that has a changing state. One way to resolve this paradox is to realize that it is the user's temporal existence that imposes state on the system. If the user could step back from the interaction and think in terms of streams of balances rather than individual transactions, the system would appear stateless. (Similarly in physics, when we observe a moving particle, we say that the position (state) of the particle is changing. However, from the perspective of the particle's world line in space-time there is no change involved.)

We began this chapter with the goal of building computational models whose structure matches our perception of the real world we are trying to model. We can model the world as a collection of separate, time-bound, interacting objects with state, or we can model the world as a single, timeless, stateless unity. Each view has powerful advantages, but neither view alone is completely satisfactory. A grand unification has yet to emerge.

Our world is modeled as an immutable, timeless, stateless unity from the perspective of physics

Frozen Block Universe and Human Consciousness

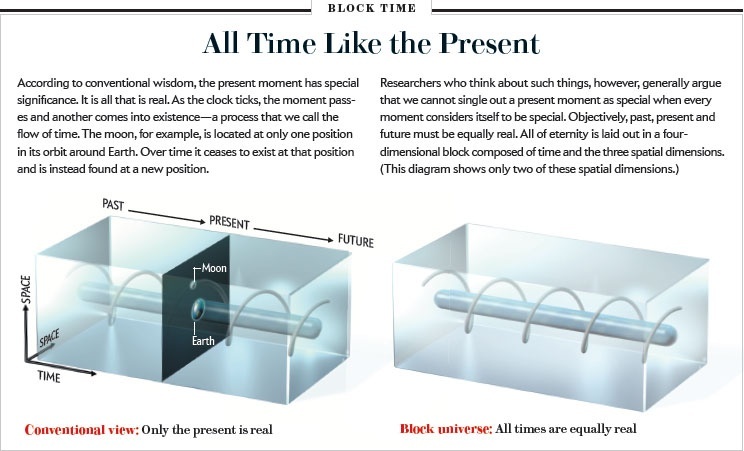
Conal Elliott(a developer who has contributed to early FRP) explaines

FRP is about "datatypes that represent a value over time ". Conventional imperative programming captures these dynamic values only indirectly, through state and mutations. The complete history (past, present, future) has no first class representation. Moreover, only discretely evolving values can be (indirectly) captured, since the imperative paradigm is temporally discrete. In contrast, FRP captures these evolving values directly and has no difficulty with continuously evolving values. Dynamic/evolving values (i.e., values "over time") are first class values in themselves. You can define them and combine them, pass them into & out of functions.

timeline as a datatype that represents a first-class value over time / a stream (infinite sequence) in JavaScript

timeline : a datatype that represents a first class value over time in JavaScript / a stream (infinite sequence) / time function as a stream / world line in space-time.

T() : timeline instance

T() is a timeline instance:

    const a = T();

timeline [now]

As timeline is an infinite stream of time, timeline has a (a user's perspective) current value: timeline[now], and can be easily get/set as below:

    a[now] = 1;
    console.log(a[now]);

1

timeline as a functor

timelinedatatype is a functor (a datatype that methods/functions always return the identical datatype, such as Array.map).

timeline has only one method/function, sync.

timeline.sync()

timeline.sync() returns a new timeline instance that a given function applied to on every update of timeline[now] in reactive manner

timeline.sync() corresponds to Array.map, but on TimeLine.

    const a = T();
    const timeline = a.sync(log);

    a[now] = 1;
    a[now] = 5;

1
5

As timeline.sync is functor:

    const a = T();
    const tl = a
      .sync(log)
      .sync(log);

    a[now] = 9;

9
9

    const a = T();
    const b = (a).sync(a => a * 2);
    const c = (a)(b).sync(([a, b]) => a + b);
    const abc = (a)(b)(c);

    const timeline = abc.sync(log);

    a[now] = 1;
    a[now] = 5;

[ 1, 2, 3 ]
[ 5, 10, 15 ]

Now, the values a and b are guaranteed to synchronize with satisfying the equation.

timeline as a monoid

A monoid is an algebraic structure with a single associative binary operation and an identity element.

In algebra,

0 is an identiy element in +(addition) operation,

    a + 0 = a  //right identity
    0 + a = a  //left identity

1 is an identity element in *(multiplication) operation,

    a ∗ 1 = a  //right identity
    1 ∗ a = a  //left identity

Associative property

   1 + 2 + 3 = 1 + 2 + 3
   (1+2) + 3 = 1 + (2+3)
       3 + 3 = 1 + 5
           6 = 6

A string is also a monoid

string + string => string

    "Hello" + " " + "world"
    = "Hello " + "world"
    = "Hello" + " world"

appears to be associative, and identity element is "".

identiy of timeline

timeline is a monoid, and the identity element of timeline is T or (T):

T(a) = a = a(T)

(T)(a) = (a) = (a)(T)

The nature of left identity: T(a) = a is especially important because we should intuitively be aware of that an instance of timeline for a given timeline instance is identical.

timeline composition

timeline is a monoid, and composable:

const a = T();
const b = T();
const ab = (a)(b); // ab is another `timeline` composed of a and b

const c = T();
const abc = (ab)(c); //  == (a)(b)(c)

associative of timeline

timeline is a monoid, and satisfies associative law:

(a)(b)(c)
= ((a)(b))(c)
= (a)((b)(c))

Timeline composition

Here we can compose timelines.

Now we have 2 equations:

   b = a * 2
   c = a + b

These equations can be easily implemented to a timeline code:

    const a = T();
    const b = a
      .sync(a => a * 2);
    const c = (a)(b)
      .sync(([a, b]) => a + b);

    const timeline = c.sync(log);

    a[now] = 1;

3

If we need a synchronized update of all of a,b,c which is an atomic update of [a,b,c],

    const a = T();
    const b = a.sync(a => a * 2);
    const c = (a)(b).sync(([a, b]) => a + b);

    const abc = (a)(b)(c);
    const tl = abc.sync(log);

    a[now] = 1;
    a[now] = 5;

[ 1, 2, 3 ]
[ 5, 10, 15 ]

The values of a,b,c are now guaranteed to synchronize with satisfying the equation.

In a practical program, in this manner, we can define dependencies of events, IO, etc., and timeline is a complete alternative of State Monad or Continuation Monad such as Promise simply because there is "no state" as discussed earlier.

Event encapsulation

When we define a timeline with an empty argument:

    const a = T();

is it really an empty timeline?

The fact is it is not empty because actually, we occasionally "manually" update the timeline value as

    a[now] = 1;

The argument of timeline in empty, Nevertheless, various inputs would happen to the timeline. In a sense, implicitly, our real-world events or time function of the world: f(t) are encapsulated to it.

    const a = T(realWorldTimeFunction);

Having said that. any event functions can be encapsulated to timeline instances.

They can be IO inputs or simply a timer event,

    const start1 = T((timeline) => {
      setTimeout(() => (timeline[now] = true), 1000);
    });
    const start2 = T((timeline) => {
      setTimeout(() => (timeline[now] = true), 2000);
    });

Obviously, the "custom" timelilne can be composed.

  (start1)(start2)
     .sync(doSomethingFunction);

Tiny library in around 100 lines

Timeline Monoid is a minimal library and the code is in around 100 lines

based on my other library free-monoid

https://www.npmjs.com/package/free-monoid

The latest code of free-monoid is hard-coded and included in the same module file of timeline-monoid.

SourceCode :

(() => {
  "use strict";
  const freeMonoid = (operator) => (() => {
  const flattenDeep = (arr1) => arr1
    .reduce((acc, val) => Array.isArray(val)
      ? acc.concat(flattenDeep(val))
      : acc.concat(val), []);
  const M = (() => { //(M)(a)(b)
    const toList = arr => arr.reduce((a, b) => (a)(b), (M));
    const m = (a) => (Array.isArray(a))
      ? toList(flattenDeep(a))
      : (!!a && !!a.M)
        ? (a)
        : (() => {
          const ma = b => (b === m) // right id
            ? (ma)
            : !b.M
              ? (ma)(M(b))
              : (() => {
                const mab = M();
                mab.units = ma.units.concat(b.units);
                mab.val = mab.units.map(unit => unit.val[0]);
                return mab; // (m)(a)(b)
              })();
          ma.M = m;
          ma.val = [a];
          ma.units = [ma];
          operator(ma);
          return ma;
        })();
    m.M = m;
    m.val = [m]; //["__IDENTITY__"];
    m.units = [m];
    operator(m);
    return (m);
  })();
  return M;
})();
  //Timeline monoid based on freeMonoid =============
  const now = "now";
  const log = (m) => {
    console.log(m);
    return m;
  };
  const mlog = (msg) => (m) => {
    console.log(msg + ": " + m);
    return m;
  };
  const _T = () => freeMonoid(operator);
  const operator = (timeline) => {
    const T = timeline.M;
    Object.defineProperties(timeline, //detect TL update
      {
        now: { //timeline[now]
          get() {
            return timeline.value[0];
          },
          set(tUpdate) {
            return (() => {
              timeline.value = [tUpdate];
              timeline._wrapF.map(f => f(tUpdate));
            })();
          }
        }
      });
    timeline.value = [];
    timeline.sync = f => {
      const syncTL = T();
      timeline._eval()._wrap(val => (syncTL[now] = f(val)));
      return syncTL;
    };
    timeline._wrapF = [];
    timeline._wrap = f => {
      timeline._wrapF[timeline._wrapF.length] = f;
      return timeline;
    };
    timeline._eval = () => (timeline.evaluated)
    || (timeline.units.length === 1)
      ? timeline
      : (() => {
        timeline.evaluated = true;
        const reset = () => timeline.units
          .map((t, i) => updates[i][now] = 0);
        const update = () => timeline[now] = timeline.units
          .map((t) => t[now]);
        const check = () => (timeline.units
          .map((t, i) => updates[i][now])
          .reduce((a, b) => (a * b)) === 1) //all updated
          ? update()
          : true;
        const updates = timeline.units
          .map((t) => T()._wrap(check));
        const dummy0 = timeline.units
          .map((t, i) => t._wrap(() => updates[i][now] = 1));
        const dummy1 = timeline._wrap(reset);
        timeline[now] = null; //initial reset
        return timeline;
      })();
    //------------------
    timeline._timeF = () => (typeof timeline.val[0]
    === "function") //_wrapped eventF
      ? timeline.val[0](timeline)
      : true;
    //non-lazy evaluate on the creation of timeF TL
    timeline._timeF();
  }; //-------operator
  const T = _T();
  //------------------
  const timeline = {
    T: T,
    now: now,
    log: log,
    mlog: mlog
  };
  //------------------
  const exporting = (typeof module === "object"
  && typeof module.exports === "object")
    ? module.exports = timeline
    : self.timeline = timeline;
//============================
})();

MIT License