Nummy

Nummy is a functional and modular number computation, description, and formatting library.

Table of Contents:

1. Usage
2. Method signatures
3. API Docs
   • string methods
   • math methods
   • casting/conversion methods
   • test/boolean methods
   • array methods
4. Advanced usage

Basic

var nummy = require('nummy');

var abbr = nummy(1100).abbr(1);
// => "1.1k"

Chained

var sixteenBitsInBytes = nummy.chain().pow(2, 16).bytes();

console.log(sixteenBitsInBytes.value());
// => "64kB"

var obj = {};
obj[sixteenBitsInBytes] = sixteenBitsInBytes.toNumber();
console.log(obj);
// => {"64kB": 65536}

Single-method

var _ = require('underscore');
var isEven = require('nummy/boolean/isEven');
var product = require('nummy/math/product');

var isProductEven = _.compose(isEven, product);

console.log(isProductEven(3, 5, 7))
// => false

A note about method signatures

You have probably noticed that different method signatures have been used above. Nummy will fill in the first argument to any method with the number it was initialized with when the method is called with fewer arguments than its full complement of arguments. This allows for greater flexibility because you can Nummy-ize a number and then call several of Nummy's methods on it:

var myNummy = nummy(4096);
console.log(myNummy.sqrt());
// => 64
console.log(myNummy.bytes());
// => 4kB
console.log(myNummy.factor());
// => [ 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048 ]

You can also initialize an empty Nummy instance and perform different operations on different numbers:

var myNummy = nummy();

console.log(myNummy.sqrt(16));
// => 4
console.log(myNummy.bytes(16384 + 128, 1));
// => 16.1kB
console.log(myNummy.factor(45));
// => [ 1, 3, 5, 9, 15 ]

Base conversion

All of the base conversion methods follow the same signature: method(number**, padTo)

• #base36: nummy(135).base36(4) => "003R"
• #binary: nummy(9740).binary(16) => "0010011000001100"
• #hex: nummy(7178).hex(8) => "00001C0A"

Format numbers according to common unit systems

• #abbr: nummy(7645).abbr(3) => "7.645k"
• #bytes: nummy(1478).bytes(2) => "1.44kB"
• #metric: nummy(6918).metric(1) => "6.9k"

All three methods take the same first two arguments, (num**, precision)--num being the number to be formatted and precision the number of decimal places to include.

Both bytes and metric also take a limit argument which indicates the highest unit symbol to represent in 1000s (or 1024s for bytes) blocks. For metric, the default is 1 meaning we stop incrementing units at 1000, which works quite well for representing grams and meters (NOTE: the 'c' or hundredths unit is skipped). For bytes, the default is 4 meaning we stop at the trillions or 'T'. The limit can be increased or set to false to allow display of higher unit symbols.

• #chr: nummy(77).chr() => "M"
• #format: nummy(8822).format([optional: {place: null, thousands: ',', decimal: '.'}]) => "8,822"
• #ordinalize: nummy(1257).ordinalize() => "1257th"
• #pad: nummy(6275).pad(8) => "00006275"

I've added a number of additional mathematical operation methods:

Single argument methods

The following methods all have a single argument signature: method(number**)

• #abs: nummy(-8635).abs() => 1
• #acos: nummy(0).acos() => 1.5707963267948966
• #asin: nummy(-0.6).asin() => -0.6435011087932844
• #atan: nummy(2).atan() => 1.1071487177940906
• #ceil: nummy(8688.5).ceil() => 8689
• #cos: nummy(1494).cos() => 0.17183612697016132
• #exp: nummy(1).exp() => 2.718281828459045
• #floor: nummy(748.9).floor() => 748
• #sin: nummy(1).sin() => 0.8414709848078965
• #sqrt: nummy(3950).sqrt() => 62.849025449882674
• #tan: nummy(1.1).tan() => 1.9647596572486523

Two argument methods

The following methods all have a two argument signature: method(number1**, number2)

• #add: (alias: plus) nummy(3137).add(1) => 3138
• #atan2: nummy(3641).atan2(0) => 1.5707963267948966
• #divide: nummy(7226).divide(2) => 0.0002767783005812344
• #divideBy: nummy(7226).divideBy(2) => 3613
• #log: nummy(3807).log() => 8.244596756382498 or nummy(3807).log(0.2) => -5.122655986097307
• #modulo: (alias: mod) nummy(4508).modulo(3) => 2
• #moduloOf: nummy(3).moduloOf(4508) => 2
• #multiply: nummy(7435).multiply(2) => 14870
• #pow: nummy(3).pow(3) => 27
• #round: nummy(65).round(-1) => 70
• #subtract: (alias: minus) nummy(5283).subtract(1) => 5282
• #subtractFrom: nummy(7908).subtractFrom(0) => -7908

Multi-argument methods

The following methods all have a multiple argument signature: method([num1**[, num2, …]])

• #max: returns the largest number amongst its arguments nummy(1347).max(1, 1253, 932) => 1347
• #min: returns the smallest number amongst its arguments nummy(8105).min(9234, 8102) => 8102
• #product: returns the result of multiplying all of its arguments together nummy(1).product(2,3,4) => 24
• #sum: returns the result of adding all of its arguments together nummy(1).sum(2,3,4) => 10

The following methods all have a single argument signature: method(number**)

• #toInteger: nummy(-735.2685004007071).toInteger() => -735
• #toInt32: nummy(759630119195208).toInt32() => 728388168
• #toUInt32: nummy(-1).toUInt32() => 4294967295
• #toNumber: nummy('-482.50145046040416').toNumber() => -482.50145046040416

Single argument methods

The following methods all have a single argument signature: method(number**)

• #isEven: nummy(5629).isEven() => false
• #isInteger: nummy(1433).isInteger() => true
• #isOdd: nummy(6296).isOdd() => false

Two argument methods

The following methods all have a two argument signature: method(number1**, number2)

• #isMultipleOf: nummy(832).isMultipleOf(3) => false
• #isFactorOf: nummy(3).isFactorOf(9933) => true

The following methods all have a single argument signature: method(number**)

• #factor: nummy(234).factor() => [ 1, 2, 3, 6, 9, 13, 18, 26, 39, 78, 117 ]

Functional programming

var _ = require('underscore');
var nummy = require('nummy');

var range = _.range(13);
var table = [];

range.forEach(function (num) {
    var myNummy = nummy(num);
    table.push(range.map(myNummy.multiply.bind(myNummy)))
});

console.table(table);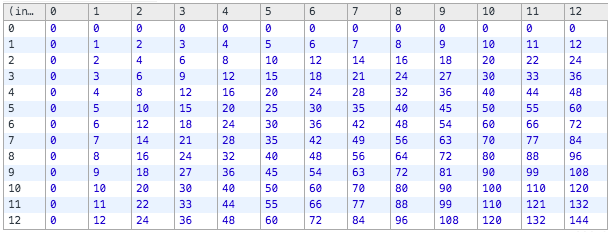

Acknowledgements

• Many thanks to Andrew Plummer for his pioneering work in creating the SugarJS number module. Many of the methods in Nummy are directly adapted from Sugar's number methods.

• Also, I owe a big "Thank you!" to Nathan Fritz for challenging me to think beyond the initial limits of Nummy 1.0.