Algorithm-Sort-Merge

About Merge Sort

Merge Sort is a Divide and Conquer algorithm. It divides input array in two halves, calls itself for the two halves and then merges the two sorted halves. The merge() function is used for merging two halves. The merge(arr, l, m, r) is key process that assumes that arr[l..m] and arr[m+1..r] are sorted and merges the two sorted sub-arrays into one.

 * Merge sort algorithm ! 
 * Class	Sorting algorithm
 * Data structure	Array
 * Worst-case performance	O(n log n) 
 * Best-case performance	O(n log n) typical, O(n) natural variant
 * Average performance	O(n log n) 
 * Worst-case space complexity О(n) total, O(n) auxiliary
 *   where n is the size of the input array.
 *   input array elements could be negative/positive and also integer or float .
 *   Note: there are another kind of Merg sort by the name of 3-way Merge Sort . 
 *         Merge sort involves recursively splitting the array into 2 parts, sorting and finally merging them. 
 *         A variant of merge sort is called 3-way merge sort where instead of splitting the array into 2 parts 
 *         we split it into 3 parts.
 *         Merge sort recursively breaks down the arrays to subarrays of size half. Similarly, 
 *         3-way Merge sort breaks down the arrays to subarrays of size one third.
 *
 * Author: Pooya Hatami

Installation

If you are using a browser, you can download node-sort-merge.js from GitHub or just bellow hotlink to it:

<script src="https://raw.githubusercontent.com/pooyahatami/Algorithm-Sort-Merge/master/node-sort-merge.js"></script>

If you are using node, you can install node-sort-merge with npm.

npm install node-sort-merge

Usage :

var nodesort = require('./node-sort-merge');
var displaymode = "No"; //"Yes";  // "Yes" for more details of algorithm progress 
...
nodesort(inputArray, displaymode, function(err,sortRef) {
        if (err) {
            // TODO error handeling 
            }
	      else {
           var result = sortRef.mergeSort(inputArray);
           // TODO output 
	            }
    });

Ruls :

• Sort Array of integers / float .
• Array's element could be negative and positive .
• Returns error mesage if not found valid input.
• Turn On details of Algorithms progress useing : displaymode = "Yes"

var displaymode = "No"; //"Yes";

Example

var nodesort = require('./node-sort-bucket');

var arrin00 = [20, 8 , -11, 12, 22 , 9 , 10 ];
var arrin01 = [20, 8 , 48, 120, 220 , 390 , 1000 ];
var arrin02 = [20, 8 , 480 , 120, 220 , 390 , 1000 ];
var arrin03 = [1120, 800 , 480 , 120, 20 , 390 , 1000 ];
var arrin04 = ['g', 'e', 'e', 'k', 's', 'f', 'o',
                      'r', 'g', 'e', 'e', 'k', 's'];
var arrin05 = [1, 3, 7, 25, 12, 9, 8,
                      121, 221, 10, 18, 29, 49];
var arrin06 = [1, 3, -7, 25, 12, 9, 8,
                      121, 221, -10, 18, 29, 49];
var arrin07 = [1, 3, 7000000000000000000, 25, 12, 9, 8,
                      121, 221, 100000000000000000000000000 , 18, 290000000000000000000, 49];
var arrin08 = [1, 3, 75432, 25, 12, 9, 8,
                      121, 221, 976562 , 18, 299999, 49];
var arrin09 = [0.897, 0.565, 0.656, 0.1234, 0.665, 0.3434 , 0.611 , 0.621 ];
var arrin10 = [1,342, 14,293 , 0.897, 0.565, 0.656, 0.1234, 0.665, 0.3434 , 0.611 , 0.621 ];
var arrin11 = [5, 8 , 11, 12, 2 , 9 , 10 , 4 , 11, 10, 12, 7, 9 ];
var arrin12 = "";


function solveSorting(inputArray) {
    var arr_original = inputArray.toString() ;
    var sortedArray = inputArray;

    nodesort(inputArray, function(err,sortRef) {
        if (err) {
	         console.log(err);
	                }
	      else {
           var result = sortRef.bucketSort(inputArray);
	         console.log("Success attempt to sort array \r\n \t ["+arr_original+" ] \r\n and result is : \r\n \t [ "
                + result + " ]" );
  
	      sortedArray = result;
	            }
	      console.log("----------------------------------------------------------"); 
    });
    
    return sortedArray;
};

solveSorting(arrin09);
solveSorting(arrin00);
solveSorting(arrin10);
solveSorting(arrin11);
solveSorting(arrin12);

See following C implementation for details.

MergeSort(arr[], l,  r)
If r > l
     1. Find the middle point to divide the array into two halves:  
             middle m = (l+r)/2
     2. Call mergeSort for first half:   
             Call mergeSort(arr, l, m)
     3. Call mergeSort for second half:
             Call mergeSort(arr, m+1, r)
     4. Merge the two halves sorted in step 2 and 3:
             Call merge(arr, l, m, r)

The following diagram from wikipedia shows the complete merge sort process for an example array {38, 27, 43, 3, 9, 82, 10}. If we take a closer look at the diagram, we can see that the array is recursively divided in two halves till the size becomes 1. Once the size becomes 1, the merge processes comes into action and starts merging arrays back till the complete array is merged.

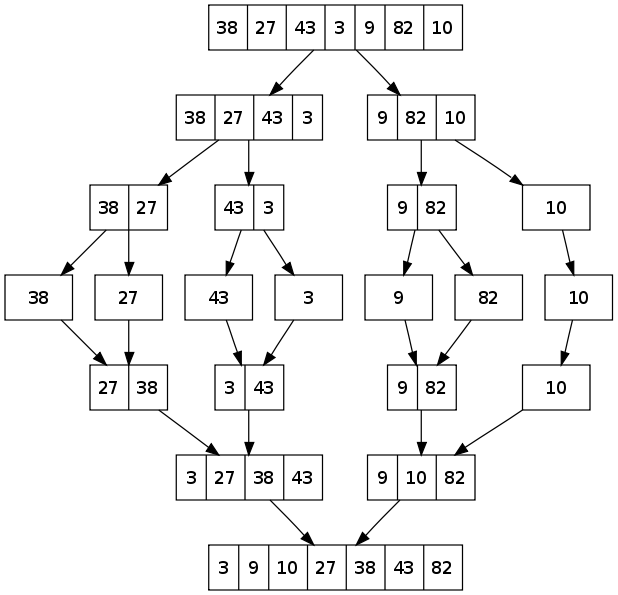
Following is C implementation of counting sort.

/* C program for Merge Sort */
#include<stdlib.h>
#include<stdio.h>
 
// Merges two subarrays of arr[].
// First subarray is arr[l..m]
// Second subarray is arr[m+1..r]
void merge(int arr[], int l, int m, int r)
{
    int i, j, k;
    int n1 = m - l + 1;
    int n2 =  r - m;
 
    /* create temp arrays */
    int L[n1], R[n2];
 
    /* Copy data to temp arrays L[] and R[] */
    for (i = 0; i < n1; i++)
        L[i] = arr[l + i];
    for (j = 0; j < n2; j++)
        R[j] = arr[m + 1+ j];
 
    /* Merge the temp arrays back into arr[l..r]*/
    i = 0; // Initial index of first subarray
    j = 0; // Initial index of second subarray
    k = l; // Initial index of merged subarray
    while (i < n1 && j < n2)
    {
        if (L[i] <= R[j])
        {
            arr[k] = L[i];
            i++;
        }
        else
        {
            arr[k] = R[j];
            j++;
        }
        k++;
    }
 
    /* Copy the remaining elements of L[], if there
       are any */
    while (i < n1)
    {
        arr[k] = L[i];
        i++;
        k++;
    }
 
    /* Copy the remaining elements of R[], if there
       are any */
    while (j < n2)
    {
        arr[k] = R[j];
        j++;
        k++;
    }
}
 
/* l is for left index and r is right index of the
   sub-array of arr to be sorted */
void mergeSort(int arr[], int l, int r)
{
    if (l < r)
    {
        // Same as (l+r)/2, but avoids overflow for
        // large l and h
        int m = l+(r-l)/2;
 
        // Sort first and second halves
        mergeSort(arr, l, m);
        mergeSort(arr, m+1, r);
 
        merge(arr, l, m, r);
    }
}
 
/* UTILITY FUNCTIONS */
/* Function to print an array */
void printArray(int A[], int size)
{
    int i;
    for (i=0; i < size; i++)
        printf("%d ", A[i]);
    printf("\n");
}
 
/* Driver program to test above functions */
int main()
{
    int arr[] = {12, 11, 13, 5, 6, 7};
    int arr_size = sizeof(arr)/sizeof(arr[0]);
 
    printf("Given array is \n");
    printArray(arr, arr_size);
 
    mergeSort(arr, 0, arr_size - 1);
 
    printf("\nSorted array is \n");
    printArray(arr, arr_size);
    return 0;
}

Following is Java implementation of counting sort.

/* Java program for Merge Sort */
class MergeSort
{
    // Merges two subarrays of arr[].
    // First subarray is arr[l..m]
    // Second subarray is arr[m+1..r]
    void merge(int arr[], int l, int m, int r)
    {
        // Find sizes of two subarrays to be merged
        int n1 = m - l + 1;
        int n2 = r - m;
 
        /* Create temp arrays */
        int L[] = new int [n1];
        int R[] = new int [n2];
 
        /*Copy data to temp arrays*/
        for (int i=0; i<n1; ++i)
            L[i] = arr[l + i];
        for (int j=0; j<n2; ++j)
            R[j] = arr[m + 1+ j];
 
 
        /* Merge the temp arrays */
 
        // Initial indexes of first and second subarrays
        int i = 0, j = 0;
 
        // Initial index of merged subarry array
        int k = l;
        while (i < n1 && j < n2)
        {
            if (L[i] <= R[j])
            {
                arr[k] = L[i];
                i++;
            }
            else
            {
                arr[k] = R[j];
                j++;
            }
            k++;
        }
 
        /* Copy remaining elements of L[] if any */
        while (i < n1)
        {
            arr[k] = L[i];
            i++;
            k++;
        }
 
        /* Copy remaining elements of R[] if any */
        while (j < n2)
        {
            arr[k] = R[j];
            j++;
            k++;
        }
    }
 
    // Main function that sorts arr[l..r] using
    // merge()
    void sort(int arr[], int l, int r)
    {
        if (l < r)
        {
            // Find the middle point
            int m = (l+r)/2;
 
            // Sort first and second halves
            sort(arr, l, m);
            sort(arr , m+1, r);
 
            // Merge the sorted halves
            merge(arr, l, m, r);
        }
    }
 
    /* A utility function to print array of size n */
    static void printArray(int arr[])
    {
        int n = arr.length;
        for (int i=0; i<n; ++i)
            System.out.print(arr[i] + " ");
        System.out.println();
    }
 
    // Driver method
    public static void main(String args[])
    {
        int arr[] = {12, 11, 13, 5, 6, 7};
 
        System.out.println("Given Array");
        printArray(arr);
 
        MergeSort ob = new MergeSort();
        ob.sort(arr, 0, arr.length-1);
 
        System.out.println("\nSorted array");
        printArray(arr);
    }
}
/* This code is contributed by Rajat Mishra */

Following is Python implementation of counting sort.

# Python program for implementation of MergeSort
 
# Merges two subarrays of arr[].
# First subarray is arr[l..m]
# Second subarray is arr[m+1..r]
def merge(arr, l, m, r):
    n1 = m - l + 1
    n2 = r- m
 
    # create temp arrays
    L = [0] * (n1)
    R = [0] * (n2)
 
    # Copy data to temp arrays L[] and R[]
    for i in range(0 , n1):
        L[i] = arr[l + i]
 
    for j in range(0 , n2):
        R[j] = arr[m + 1 + j]
 
    # Merge the temp arrays back into arr[l..r]
    i = 0     # Initial index of first subarray
    j = 0     # Initial index of second subarray
    k = l     # Initial index of merged subarray
 
    while i < n1 and j < n2 :
        if L[i] <= R[j]:
            arr[k] = L[i]
            i += 1
        else:
            arr[k] = R[j]
            j += 1
        k += 1
 
    # Copy the remaining elements of L[], if there
    # are any
    while i < n1:
        arr[k] = L[i]
        i += 1
        k += 1
 
    # Copy the remaining elements of R[], if there
    # are any
    while j < n2:
        arr[k] = R[j]
        j += 1
        k += 1
 
# l is for left index and r is right index of the
# sub-array of arr to be sorted
def mergeSort(arr,l,r):
    if l < r:
 
        # Same as (l+r)/2, but avoids overflow for
        # large l and h
        m = (l+(r-1))/2
 
        # Sort first and second halves
        mergeSort(arr, l, m)
        mergeSort(arr, m+1, r)
        merge(arr, l, m, r)
 
 
# Driver code to test above
arr = [12, 11, 13, 5, 6, 7]
n = len(arr)
print ("Given array is")
for i in range(n):
    print ("%d" %arr[i]),
 
mergeSort(arr,0,n-1)
print ("\n\nSorted array is")
for i in range(n):
    print ("%d" %arr[i]),
 
# This code is contributed by Mohit Kumra

Output:

Given array is
12 11 13 5 6 7

Sorted array is
5 6 7 11 12 13

Other Sorting Algorithms :

• Selection Sort
• Bubble Sort
• Insertion Sort
• Merge Sort
• Heap Sort
• QuickSort
• Counting Sort
• Bucket Sort
• ShellSort

References:

• https://en.wikipedia.org/wiki/Merge_sort/
• http://www.geeksforgeeks.org/merge-sort/
• http://www.codecodex.com/wiki/Merge_sort