Algorithm-Sort-Bucket (or bin sort)

About Bucket Sort

Bucket sort is mainly useful when input is uniformly distributed over a range. For example, consider the following problem. Sort a large set of floating point numbers which are in range from 0.0 to 1.0 and are uniformly distributed across the range. How do we sort the numbers efficiently?

 * Bucket sort algorithm ! (or bin sort)
 * Class	Sorting algorithm
 * Data structure	Array
 * Worst-case performance	O(n^{2}) 
 * Best-case performance	Omega(n+k) 
 * Average performance	Theta(n+k) 
 * Worst-case space complexity O(n\cdot k)
 *   where n is the size of the input array.
 *   Note: Bucket sort can be seen as a generalization of counting sort; in fact, if each bucket has size 1 then 
 *         bucket sort degenerates to counting sort. The variable bucket size of bucket sort allows it to use O(n) 
 *         memory instead of O(M) memory, where M is the number of distinct values; in exchange, it gives up 
 *         counting sort s O(n + M) worst-case behavior.
 *
 * Author: Pooya Hatami

Installation

If you are using a browser, you can download node-sort-bucket.js from GitHub or just bellow hotlink to it:

<script src="https://raw.githubusercontent.com/pooyahatami/Algorithm-Sort-Bucket/master/node-sort-bucket.js"></script>

If you are using node, you can install node-sort-bucket with npm.

npm install node-sort-bucket

Usage :

var nodesort = require('./node-sort-bucket');
var displaymode = "No"; //"Yes";  // "Yes" for more details of algorithm progress 
...
nodesort(inputArray, displaymode, function(err,sortRef) {
        if (err) {
            // TODO error handeling 
            }
	      else {
           var result = sortRef.bucketSort(inputArray);
           // TODO output 
	            }
    });

Ruls :

• Sort Array of integers (Decimal Base 10 , Hex Base 16 , Octal Base 8 , Binary Base 2 ).
• Array's element shoud be integers and not beager than 999,999 .
• Returns the Sorted Array or -1 if not found valid input.
• Turn On details of Algorithms progress useing : displaymode = "Yes"

var displaymode = "No"; //"Yes";

Example

var nodesort = require('./node-sort-bucket');

var arrin00 = [20, 8 , -11, 12, 22 , 9 , 10 ];
var arrin01 = [20, 8 , 48, 120, 220 , 390 , 1000 ];
var arrin02 = [20, 8 , 480 , 120, 220 , 390 , 1000 ];
var arrin03 = [1120, 800 , 480 , 120, 20 , 390 , 1000 ];
var arrin04 = ['g', 'e', 'e', 'k', 's', 'f', 'o',
                      'r', 'g', 'e', 'e', 'k', 's'];
var arrin05 = [1, 3, 7, 25, 12, 9, 8,
                      121, 221, 10, 18, 29, 49];
var arrin06 = [1, 3, -7, 25, 12, 9, 8,
                      121, 221, -10, 18, 29, 49];
var arrin07 = [1, 3, 7000000000000000000, 25, 12, 9, 8,
                      121, 221, 100000000000000000000000000 , 18, 290000000000000000000, 49];
var arrin08 = [1, 3, 75432, 25, 12, 9, 8,
                      121, 221, 976562 , 18, 299999, 49];
var arrin09 = [0.897, 0.565, 0.656, 0.1234, 0.665, 0.3434 , 0.611 , 0.621 ];
var arrin10 = [1,342, 14,293 , 0.897, 0.565, 0.656, 0.1234, 0.665, 0.3434 , 0.611 , 0.621 ];
var arrin11 = [5, 8 , 11, 12, 2 , 9 , 10 , 4 , 11, 10, 12, 7, 9 ];
var arrin12 = "";


function solveSorting(inputArray) {
    var arr_original = inputArray.toString() ;
    var sortedArray = inputArray;

    nodesort(inputArray, function(err,sortRef) {
        if (err) {
	         console.log(err);
	                }
	      else {
           var result = sortRef.bucketSort(inputArray);
	         console.log("Success attempt to sort array \r\n \t ["+arr_original+" ] \r\n and result is : \r\n \t [ "
                + result + " ]" );
  
	      sortedArray = result;
	            }
	      console.log("----------------------------------------------------------"); 
    });
    
    return sortedArray;
};

solveSorting(arrin09);
solveSorting(arrin00);
solveSorting(arrin10);
solveSorting(arrin11);
solveSorting(arrin12);

A simple way is to apply a comparison based sorting algorithm. The lower bound for Comparison based sorting algorithm (Merge Sort, Heap Sort, Quick-Sort .. etc) is Ω(n Log n), i.e., they cannot do better than nLogn. Can we sort the array in linear time? Counting sort can not be applied here as we use keys as index in counting sort. Here keys are floating point numbers.

The idea is to use bucket sort. Following is bucket algorithm.

bucketSort(arr[], n)

1) Create n empty buckets (Or lists).
2) Do following for every array element arr[i].
.......a) Insert arr[i] into bucket[n*array[i]]
3) Sort individual buckets using insertion sort.
4) Concatenate all sorted buckets.

Following diagram (taken from CLRS book) demonstrates working of bucket sort.

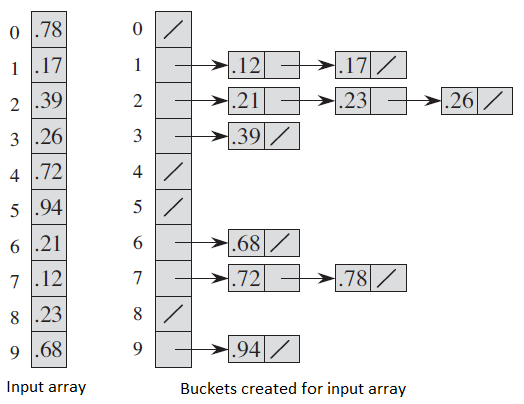
Following is C++ implementation of the above algorithm.

// C++ program to sort an array using bucket sort
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
 
// Function to sort arr[] of size n using bucket sort
void bucketSort(float arr[], int n)
{
    // 1) Create n empty buckets
    vector<float> b[n];
    
    // 2) Put array elements in different buckets
    for (int i=0; i<n; i++)
    {
       int bi = n*arr[i]; // Index in bucket
       b[bi].push_back(arr[i]);
    }
 
    // 3) Sort individual buckets
    for (int i=0; i<n; i++)
       sort(b[i].begin(), b[i].end());
 
    // 4) Concatenate all buckets into arr[]
    int index = 0;
    for (int i = 0; i < n; i++)
        for (int j = 0; j < b[i].size(); j++)
          arr[index++] = b[i][j];
}
 
/* Driver program to test above funtion */
int main()
{
    float arr[] = {0.897, 0.565, 0.656, 0.1234, 0.665, 0.3434};
    int n = sizeof(arr)/sizeof(arr[0]);
    bucketSort(arr, n);
 
    cout << "Sorted array is \n";
    for (int i=0; i<n; i++)
       cout << arr[i] << " ";
    return 0;
}

Following is Java implementation of the above algorithm.

// Bucket sort Java implementation
public void bucketsort(int[] input) {
  //get hash codes
  final int[] code = hash(input);
  //create and initialize buckets to ArrayList: O(n)
  List<Integer>[] buckets = new List[code[1]];
  for (int i = 0; i < code[1]; i++) {
    buckets[i] = new ArrayList<Integer>();
  }
  //distribute data into buckets: O(n)
  for (int i : input) {
    buckets[hash(i, code)].add(i);
  }
  /**
   * Sort each bucket: O(n).
   * I mentioned above that the worst case for bucket sort is counting
   * sort. That's because in the worst case, bucket sort may end up
   * with one bucket per key. In such case, sorting each bucket would
   * take 1^2 = O(1). Even after allowing for some probabilistic
   * variance, to sort each bucket would still take 2-1/n, which is
   * still a constant. Hence, sorting all the buckets takes O(n).
   ***/
  for (List bucket : buckets) {
    Collections.sort(bucket);
  }
  int ndx = 0;
  //merge the buckets: O(n)
  for (int b = 0; b < buckets.length; b++) {
    for (int v : buckets[b]) {
      input[ndx++] = v;
    }
  }
}
 
private int[] hash(int[] input) {
  int m = input[0];
  for (int i = 1; i < input.length; i++) {
    if (m < input[i]) {
      m = input[i];
    }
  }
  return new int[]{m, (int) Math.sqrt(input.length)};
}
 
private int hash(int i, int[] code) {
  return (int) ((double) i / code[0] * (code[1] - 1));
}
/* This code is contributed by Pooya Hatami*/

Following is Python implementation of the above algorithm.

# Python program for implementation of Bead Sort
# This code is contributed by Pooya Hatami

Output:

Sorted array is
0.1234 0.3434 0.565 0.656 0.665 0.897

Other Sorting Algorithms :

• Selection Sort
• Bubble Sort
• Insertion Sort
• Merge Sort
• Heap Sort
• QuickSort
• Counting Sort
• Radix Sort
• Bead Sort
• Bucket Sort
• ShellSort

References:

• https://en.wikipedia.org/wiki/Bucket_sort
• http://www.geeksforgeeks.org/bucket-sort-2/
• http://www.wikiwand.com/en/Bucket_sort
• http://www.geekviewpoint.com/java/sorting/bucketsort