2d-bicubic-interpolate
v1.0.7
Published
Interpolate data set representing function of two variables z = f(x,y) with bicubic spline
Maintainers
Readme
2d-bicubic-interpolate
Ver. 1.0.7
This version includes contribution of Akshat Khare. According to Akshat pull request:
Previously the code failed for matrices with repeated value of z for
different record, which is undesired, so changed the code to accomodate
that issue.Description
This package is a simple implementation of a cubic-spline by morganherlocker for two-directional interpolation (2-dimensional arrays).
Assumed purpose of this package is to interpolate discrete function of two variables (e.g., for a surface plot).
z = f(x,y)Following package was developed for another project that utilizes it for surface plot interpolation.
Dependencies
Package runs thanks to two dependencies. Firstly, of course cubic-spline by morganherlocker must be included. Another little package needed to run 2d-bicubic-spline is split-array by Arthur Verschaeve. Development dependencies fot testing include Mocha & Chai.
Install
To install package:
npm install --save 2d-bicubic-interpolateInclude in your project
import interpolateArray from '2d-bicubic-interpolate';API
interpolateArray(data, n);
Function takes two parameters: data, including data set to interpolate, and parameter n that describes 'strength' of interpolation. Function returns interpolated data set.
data
Data set is expected to be representation of a discrete function of two variables. Data set is expected to be an array of objects, where every each object presents coordinates for each point of function. Coordinates values are expected to be real numbers.
const data = [
{
x: 0,
y: 0,
z: 2
},
{
x: 1,
y: 0,
z: 0.3
},
{
x: 0,
y: 1,
z: 1.4
},
{
x: 1,
y: 1,
z: 2.5
}
]n parameter - the interpolation factor
Interpolation factor, the n parameter need to be a positive integer or 0. This number describes how many new points are going to be put between primary points. E.g., for n = 4, between every 2 primary points from input data, four new points are going to be calculated and inserted between. For n = 0, no interpolation is applied and output is the same as input.
Output
Function interpolateArray returns new data set, which has the same structure as an input. Length of new data array is described as:
L1 = L0 + (L0 - 1) * nWhere:
L1 - length of output array
L0 - length of input array
n - interpolation factor
Examples
Example 1
import interpolateArray from '2d-bicubic-interpolate';
const data = [
{
x: 0,
y: 0,
z: 0.3
},
{
x: 1,
y: 0,
z: 1.2
},
{
x: 0,
y: 1,
z: 1.4
},
{
x: 1,
y: 1,
z: 2.2
}
];
console.log(interpolateArray(data, 1));
/*
console:
(9) [{…}, {…}, {…}, {…}, {…}, {…}, {…}, {…}, {…}]
0:{x: 0, y: 0, z: 0.3}
1:{x: 0, y: 0.5, z: 0.85}
2:{x: 0, y: 1, z: 1.4}
3:{x: 0.5, y: 0, z: 0.75}
4:{x: 0.5, y: 0.5, z: 1.275}
5:{x: 0.5, y: 1, z: 1.8}
6:{x: 1, y: 0, z: 1.2}
7:{x: 1, y: 0.5, z: 1.7}
8:{x: 1, y: 1, z: 2.2}
*/
Example 2
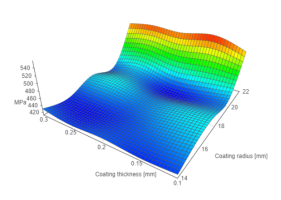
Working principle of algorithm is presented by a 3D surface chart (vis.js), representing some discrete function of two-variables.
Data before interpolation:
InterpolateArray(data, 0); 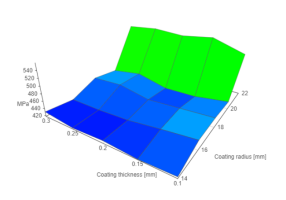
Data interpolated with different interpolation factors: Data interpolated with different interpolation factors:
InterpolateArray(data, 1); 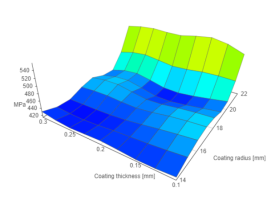
InterpolateArray(data, 10);